17425번: 약수의 합
두 자연수 A와 B가 있을 때, A = BC를 만족하는 자연수 C를 A의 약수라고 한다. 예를 들어, 2의 약수는 1, 2가 있고, 24의 약수는 1, 2, 3, 4, 6, 8, 12, 24가 있다. 자연수 A의 약수의 합은 A의 모든 약수를 더
www.acmicpc.net
목차
- 사전 지식
- 문제 접근
- 풀이1 (Accepted)
- 풀이2 (Memory Limit Exceeded)
- 풀이3 (Accepted)
사전 지식
문제 접근
자연수가 $\small{N}$ 주어지면 $\small{g(N) = f(1) + (2) + \cdots + f(N)}$를 구하면 된다. ($\small{1 \leq N \leq 10^6}$)
($\small{f(x)}$는 $\small{x}$에 대한 약수의 합이다.)
예를 들어, $\small{f(12)}$는 12의 약수가 1, 2, 3, 4, 6, 12이므로 28이다.
또한, 이러한 과정을 테스트 케이스 $\small{T}$번 수행해야 한다. ($\small{1 \leq T \leq 10^5}$)
$\small{g(x)}$를 구하려면 얼마나 걸릴까?
$\small{f(x)}$를 구하려면 $\small{[1, \sqrt{x}]}$ 범위의 수에 대해 탐색을 하면 된다. (이해가 안 된다면 여기에서 약수의 성질 부분을 참고하기 바란다.)
$\small{g(N)}$을 구할 때 $\small{N=10^6 \ }$라면 $\small{f(1), f(2), \cdots, f(10^6)}$을 모두 구해야 한다.
이를 구하는 시간 복잡도의 상한은 넉넉하게 $\small{O(10^6 \cdot \sqrt{10^6}) = O(10^9)}$이라고 할 수 있다.
실제 시간 복잡도는 $\small{f(x)}$를 구하는 평균 연산이 $\small{10^3}$보다는 작기 때문에 더 빠르다.
테스트 케이스의 개수가 중요할까?
테스트 케이스의 개수 $\small{T}$는 중요한 요소가 아니다.
왜냐하면, 모든 $\small{g(x)}$를 배열을 통해서 저장해 테스트 케이스는 $\small{O(1)}$만에 처리가 가능하기 때문이다.
따라서, 최종 시간 복잡도는 상한 $\small{O(10^9)}$라고 할 수 있으며, 문제의 시간제한이 1초이므로 TLE(Time Limit Exceeded)가 나게 된다.

풀이1 (Accepted)
가장 간단한 풀이이자, 이 문제에 대해 출제자가 의도한 풀이라고 생각한다.
이 풀이는 $\small{f(x)}$를 기준으로 문제를 생각하는 것이 아닌 약수가 될 수 있는 숫자를 기준으로 생각한다.
즉, '약수 $c$를 어떤 $\small{f(x)}$가 포함하고 있을까?' 로 접근하는 것이다.
이렇게 하면 모든 약수의 후보 $1 \leq c \leq 10^6$에 대해서만 살펴보면 모든 $\small{f(x)}$를 구할 수 있다.
이는 에라토스테네스의 체 알고리즘을 수행하는 과정과 매우 비슷하며 따라서 시간 복잡도의 상한은 $\small{O(21 \cdot 10^6)}$이다.
에라토스테네스의 체 알고리즘의 반복문에서 $\small{c=i}$일 때 연산 횟수는 $\frac{10^6}{i}$이다.
$\small{1 \leq c \leq 10^6}$에 대해 살펴봐야 하므로 총 연산 횟수는 $ \frac{10^6}{1} + \frac{10^6}{2} + \cdots + \frac{10^6}{10^6} $이다.
즉, 총 시간 복잡도는 $ \frac{10^6}{1} + \frac{10^6}{2} + \cdots + \frac{10^6}{10^6} $의 상한을 구하면 된다.
위 식을 $\small{10^6}$으로 묶으면 $10^6 \cdot (\frac{1}{1} + \frac{1}{2} + \cdots \frac{1}{10^6})$와 같이 나타낼 수 있다.
따라서, 우리는 $(\frac{1}{1} + \frac{1}{2} + \cdots \frac{1}{10^6})$ 의 상한 $\small{k}$를 구하면 된다.
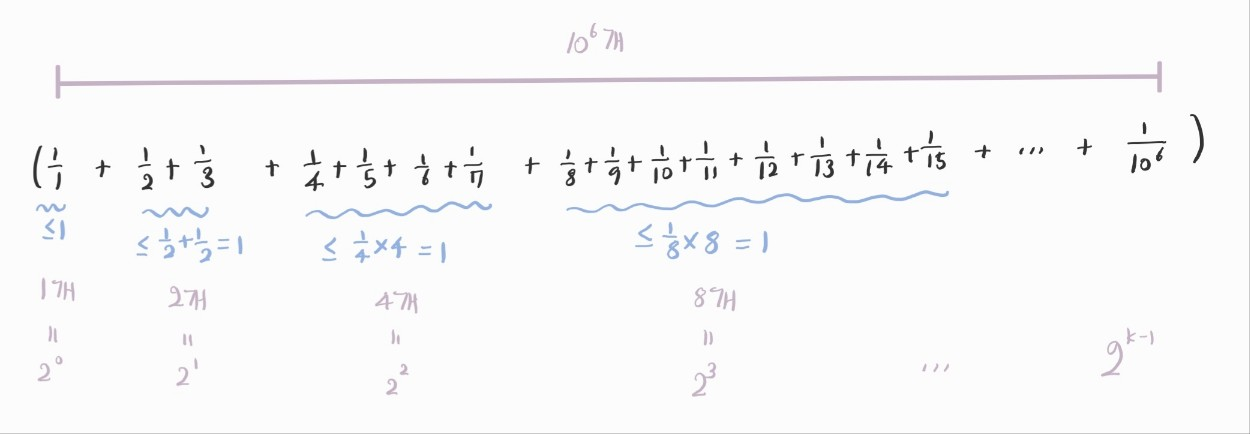
위와 같이 나오므로 $\sum_{\small{i=0}}^{\small{i=k-1}} (2^i) = 10^6$을 계산하면 $\small{k}$를 구할 수 있다.
이는 등비급수의 합 공식을 이용하면 $\small{k \approx 21}$임을 알 수 있다.

풀이2 (Memory Limit Exceeded)
풀이2와 풀이3은 $\small{f(x)}$를 한 번에 완성하는 게 아닌 차근차근 완성시켜 나가는 풀이이다.
풀이2는 $\small{x}$에 대해 $\small{f(x)}$, $\small{g(x)}$ 정보와 더불어 $\small{x}$에 대한 약수들의 정보(집합 자료형)를 저장하여 효율적으로 $\small{f(x)}$를 구하려 시도한 풀이이다.
$\small{x}$의 약수들을 알고 있다면 $\small{x}$의 배수 $\small{x \cdot p}$의 약수들을 효율적으로 찾을 수 있지 않을까?
결론은, $\small{x \cdot p}$의 약수들은 $\small{x}$의 약수들과 $x$의 각 약수들에 $\small{p}$를 곱한 값들로 구성된다.
하지만, 이 풀이는 $\small{1 \leq c \leq 10^6}$인 수에 대해 약수들의 집합을 저장해야 하므로 MLE(Memory Limit Exceeded)가 나게 된다.

풀이3 (Accepted)
풀이3은 소인수분해의 성질을 이용하여 $f(x)$의 값을 차근차근 완성시켜 나가는 풀이이다.
이 풀이를 이해하려면, $\small{x}$의 약수들은 소인수분해한 소수들의 곱의 조합이라는 사실을 알아야 한다. (링크)
우리가 원하는 것은 $\small{f(1), f(2), \cdots, f(x-1)}$의 정보를 이용하여 $\small{f(x)}$를 쉽게 구하는 것이다.
$\small{x}$를 소인수분해한 정보와 $\small{f(1), f(2), \cdots, f(x-1)}$ 이용해서 $\small{f(x)}$를 구할 수 없을까?
36를 소인수분해한 결과와 약수의 종류는 아래와 같다.
ㆍ 소인수분해: $\small{2^2 \times 3^2 \times 1}$
ㆍ 약수의 종류: $\small{(1, \ 2, \ 3, \ 4, \ 6, \ 9, \ 12, \ 18, \ 36)}$
72를 소인수분해한 결과와 약수의 종류는 아래와 같다.
ㆍ 소인수분해: $\small{2^3 \times 3^2 \times 1}$
ㆍ 약수의 종류: $\small{(1, \ 2, \ 3, \ 4, \ 6, \ \color{CadetBlue}8, \ 9, \ 12, \ 18, \ \color{CadetBlue}{24}, \ 36, \ \color{CadetBlue}{72})}$
72의 약수는 36에 2를 곱함으로써 생길 수 있는 조합들을 살펴보면 구할 수 있다.
즉, 위에서 보면 36에 2를 곱함으로써 $\small{(2^3 \cdot 1)}$, $\small{(2^3 \cdot 3^1)}$, $\small{(2^3 \cdot 3^2)}$ 가 약수에 추가되는 것이다.
추가된 약수들의 합은 $\small{2^3 \cdot (1 + 3^1 + 3^2)}$이며, $\small{(1 + 3^1 + 3^2)}$는 $\small{9}$의 약수들의 합이기 때문에 $\small{f(9)}$로 구할 수 있다.
즉 $\small{f(72) = f(32) + 2^3 \cdot f(9)}$ 로 구할 수 있는 것이다.

'✏️ 알고리즘 > PS 기록' 카테고리의 다른 글
| [백준 10220번] Self Representing Seq (1) | 2023.05.17 |
|---|---|
| [백준 13275번] 가장 긴 팰린드롬 부분 문자열 (1) | 2023.05.15 |
| [백준 1395번] 스위치 (2) | 2023.04.03 |
| [백준 17353번] 하늘에서 떨어지는 1, 2, ..., R-L+1개의 별 (2) | 2023.04.02 |
| [백준 12844번] XOR (0) | 2023.04.02 |
