안녕하세요 Gliver 입니다.
이번 글에서는 에라토스테네스의 체 알고리즘에 대해 알아보겠습니다.
목차
- 에라토스테네스의 체 알고리즘
- 실제 문제에서 에라토스테네스의 체 알고리즘
에라토스테네스의 체 알고리즘
에라토스테네스의 체 알고리즘은 소수(Prime Number)를 판별하는 알고리즘입니다.
소수 : 약수가 1과 자기 자신뿐인 자연수
좀 더 자세히 말하자면, 자연수 N에 대해 에라토스테네스의 체 알고리즘을 수행하고 나면,
2~N 범위의 자연수는 O(1) 만에 소수(Prime Number)인지를 판별할 수 있습니다.
에라토스테네스의 체 알고리즘을 알아보기 전에, 약수의 성질에 대해 알아보겠습니다.
약수의 성질
어떤 자연수 n이 있을 때, n의 약수 A, B에 대해 n = A x B 형태로 나타낼 수 있습니다.
ex) n = 8일 때, 약수는 [1, 2, 4, 8] 이므로
n(8) = 1 x 8 또는
n(8) = 2 x 4 으로 표현 가능
그렇다면, n = A x B 에서 min(A, B) 가 최대가 되는 상황은 언제일까요?
쉽게 말해, n을 두 수의 곱으로 나타내었을 때 두 수 중에서 작은 값이 최대가 되는 상황을 의미
ex) n = 16 일 때, 약수는 [1, 2, 4, 8 ,16]
n(16) = 1 x 16 : min(A, B) = 1
n(16) = 2 x 8 : min(A, B) = 2
n(16) = 4 x 4 : min(A, B) = 4
이므로, min(A, B) 의 최댓값은 4임.
min(A, B) 가 최대가 되려면 A와 B의 차이가 적어야 하므로 A = B 인 상황(A = B = √n) 일 것입니다.
따라서, A, B 둘 중 하나는 √n 이하이기 때문에 1부터 √n 이하인 자연수에 대해서만 살펴보면,
n = A x B 인 모든 경우를 살펴볼 수 있습니다.
ex) n=20 인 경우에,
√n = √20 = 4.xxx 이므로 1부터 4에 대해서만 살펴보면 n의 약수들을 모두 찾을 수 있다.
1인 경우 : 20 / 1 은 나머지가 0이므로 1과 20은 n(20)의 약수이다.
2인 경우 : 20 / 2 는 나머지가 0이므로 2와 10은 n(20)의 약수이다.
3인 경우 : 20 / 3 은 나머지가 0이 아니므로 건너뛴다.
4인 경우 : 20 / 4 는 나머지가 0이므로 4와 5는 n(20)의 약수이다.
따라서, n(20)의 약수는 1, 2, 4, 5, 10, 20 이 존재한다.
따라서, 어떤 자연수 n이 소수인지를 판별하려면 n을 2~√n 으로 나누면서 나누어 떨어지는지를 확인하면 됩니다.
한 번이라도 나누어 떨어지면 1과 n을 제외한 약수가 존재한다는 의미이므로 소수(Prime Number)가 아님.
에라토스테네스의 체 알고리즘
자연수 N까지 소수를 판별한다고 했을 때,
자연수 i에 대해 다음과 같은 과정을 반복합니다. (2 ≤ i ≤ √N)
ㆍ i를 제외한 i의 배수를 소수에서 제외시킵니다.
ㆍ i에 1을 더합니다.
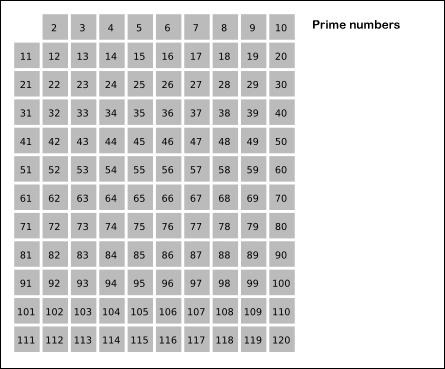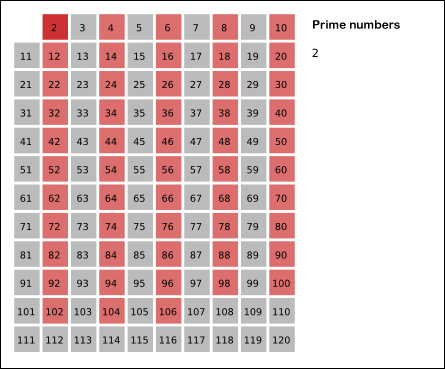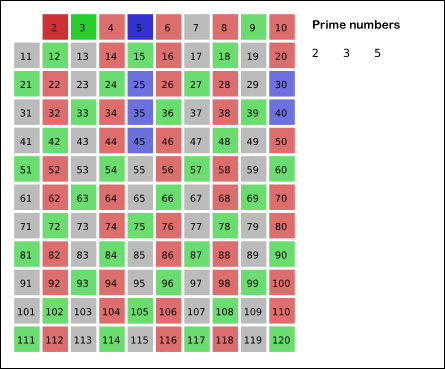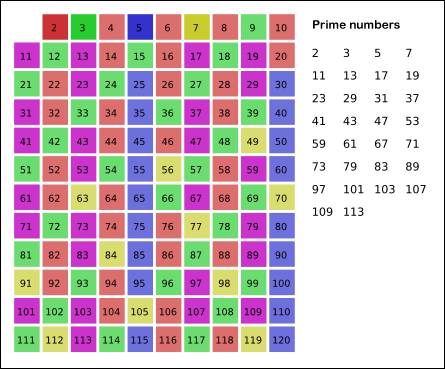
위의 N=120인 경우 에라토스테네스의 체 알고리즘을 코드로 구현하면 다음과 같습니다.
에라토스테네스의 체 알고리즘의 시간 복잡도는 $O(N \cdot log(log \ N))$ 으로 선형 시간에 가깝습니다.
실제 문제에서 에라토스테네스의 체 알고리즘
실제 문제에서 에라토스테네스의 체 알고리즘이 쓰이는 경우는 명확합니다.
위에서 배웠듯이, 여러 수에 대해 소수를 판별해야 할 때 사용하면 됩니다.
어려운 문제로 갈수록, 에라토스테네스의 체 알고리즘만 쓰는 경우는 드물고 보조적인 알고리즘으로 많이 쓰임.
[관련 문제]
궁금한 점이나 코멘트는 댓글로 남겨주세요!
- 알고리즘 공부법 : https://gliver.tistory.com/6
- 알고리즘 목차 : https://gliver.tistory.com/7
'✏️ 알고리즘 > 기본 알고리즘' 카테고리의 다른 글
| [06강] 순열 알고리즘 (0) | 2022.01.16 |
|---|---|
| [05강] 조합 알고리즘 (2) | 2022.01.10 |
| [04강] 유클리드 알고리즘 (0) | 2022.01.07 |
| [02강] 나머지(모듈러, modulo) 연산 (0) | 2022.01.02 |
| [01강] 시간 복잡도 (0) | 2022.01.02 |

![[03강] 에라토스테네스의 체 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbvr8Od%2FbtrpYmL29cZ%2FZ9F3Lf8b6cZuTBwsb6RFY0%2Fimg.gif)