안녕하세요 Gliver 입니다.
이번 글에서는 그래프(Graph) 기본에 대해 알아보겠습니다.
목차
- 그래프를 코드로 표현하기
- 인접 리스트 (Adjacency List)
- 인접 행렬 (Adjacency Matrix)
- 간선 리스트 (Edge List)
- 정리
지난 글에서 그래프는 노드(정점)와 간선으로 이루어져 있다고 설명하였습니다.
이번 글에서는 이러한 그래프를 어떻게 코드로 표현할 수 있는지 알아봅시다.
그래프를 코드로 표현하기
그래프를 코드로 어떻게 표현할 수 있을까?

그래프는 노드와 간선으로 구성되어 있으므로 노드와 간선을 각각 어떻게 표현할 수 있는지 살펴보자.
노드는 하나의 정점으로 노드의 개수만큼의 공간으로 표현할 수 있다.
간선은 노드와 노드를 선을 잇는 것이므로 간선 1개는 노드 2개로 표현할 수 있다.
이렇게 살펴본 노드와 간선의 특징에 따라 그래프를 표현하면 다음과 같이 3가지 방법이 존재하게 된다.
인접 리스트 (Adjacency List)
이 방법은 노드의 개수만큼의 공간을 확보한 뒤에 각 노드를 기준으로 연결된 노드를 저장하는 방식이다.
인접 행렬 (Adjacency Matrix)
이 방법은 '노드의 개수$\times$노드의 개수' 만큼의 행렬(공간)을 만든 후에 간선을 표현하는 방식이다.
간선 리스트 (Edge List)
이 방법은 간선의 정보만을 표현하는 방식으로 간선에 대한 정보만(노드 2개로 표현)을 저장하는 방식이다.
그래프를 코드로 표현하는 방법을 알아보기 전에 방향 그래프, 양방향 그래프와 가중 그래프에 대한 개념을 짚고 가자.
이 3가지 개념은 간선이 어떠한 특징을 갖느냐에 따라서 구분된다
방향 그래프

노드 A와 노드 B를 잇는 간선이 한 방향으로만(그림에선 A에서 B로) 갈 수 있을 때 이러한 그래프를 방향 그래프라고 한다.
양방향 그래프

노드 A와 노드 B를 잇는 간선이 A에서 B로, B에서 A로 양방향으로 갈 수 있을 때 이러한 그래프를 양방향 그래프라고 한다.
참고로, 양방향 그래프 한 개의 간선은 아래와 같이 방향 그래프 두 개의 간선으로 생각할 수도 있다.

가중 그래프

간선에 가중치가 존재한다면 이러한 그래프를 가중 그래프라고 한다.
양방향 그래프와 방향 그래프가 대립되는 개념이었다면, 가중 그래프는 이 둘과 양립할 수 있는 개념이다
이제 위에서 언급한 인접 리스트, 인접 행렬, 간선 리스트에 대해서 하나씩 살펴볼 것이다.
각각의 방법에 대해 양방향 그래프, 방향 그래프, 가중 그래프에 따라 어떻게 표현하는지도 함께 살펴보겠다.
인접 리스트 (Adjacency List)
인접 리스트는 노드의 개수만큼의 공간을 확보한 뒤에 각 노드를 기준으로 연결된 노드를 저장하는 방식이라고 하였다.
다음과 같은 그래프를 인접 리스트로 표현해보자.

위의 그래프를 인접 리스트로 표현하면 다음과 같은 2차원 배열이 만들어지게 된다.

이러한 배열을 만들고 나면 인덱스를 통해 해당 노드와 연결된 노드를 알 수 있다.
이를 코드로 표현하면 다음과 같다.
만약, 위의 그래프가 양방향 그래프라면?
답은 간단하다. 양방향 그래프 하나의 간선에 대해 아래와 같이 생각하여 인접 리스트를 만들면 된다.

만약, 위의 그래프가 가중 그래프라면?
가중 그래프라면 간선에 대해서 가중치가 얼마인지를 함께 저장하면 된다.
가중 그래프가 아닌 경우의 인접 리스트에서는 {연결된 노드}만 저장했다면,
가중 그래프인 경우의 인접 리스트에서는 {연결된 노드, 간선의 가중치} 형태로 저장하면 된다.
인접 행렬 (Adjacency Matrix)
인접 행렬은 '노드의 개수$\times$노드의 개수' 만큼의 행렬(공간)을 만든 후에 간선을 표현하는 방식이라고 하였다.
다음과 같은 그래프를 인접 행렬로 표현해보자.

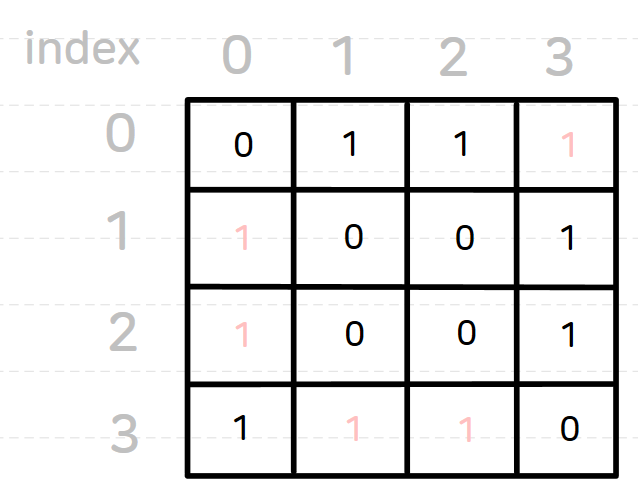
위의 그래프를 인접 행렬로 표현하면 다음과 같이 '노드의 개수$\times$노드의 개수' 크기의 2차원 배열이 만들어지게 된다.

adj_matrix[A][B]가 1이면 노드 A에서 B로 가는 간선이 있다는 의미이고, 0이면 그러한 간선이 없다는 의미이다.
이러한 배열을 만들고 나면 노드 A에서 노드 B로 가는 간선이 있는지를 adj_matrix[A][B]를 접근함으로써 알 수 있다.
노드 A와 연결된 노드를 모두 확인하고 싶다면 adj_matrix[A]에 대해 탐색해야 하므로 '노드의 개수' 만큼의 연산이 필요하다
이를 코드로 표현하면 다음과 같다.
만약, 위의 그래프가 양방향 그래프라면?
양방향 그래프 하나의 간선에 대해 방향 그래프 간선 2개로 생각하여 다음과 같이 표현하면 된다.
만약, 위의 그래프가 가중 그래프라면?
가중 그래프가 아닌 경우에, 간선이 없는 경우는 0, 있는 경우는 1로 표현하였다면,
가중 그래프인 경우에, 간선이 없는 경우는 0으로 표현하고 간선이 있는 경우는 가중치 값으로 표현하면 된다.
간선 리스트 (Edge List)
간선 리스트는 간선의 정보만을 저장하는 방식으로 '간선의 개수' 크기의 배열이 만들어진다.
다음과 같은 그래프를 간선 리스트로 표현해보자.

위의 그래프를 간선 리스트로 표현하면 다음과 같이 '간선의 개수' 크기의 1차원 배열이 만들어지게 된다.
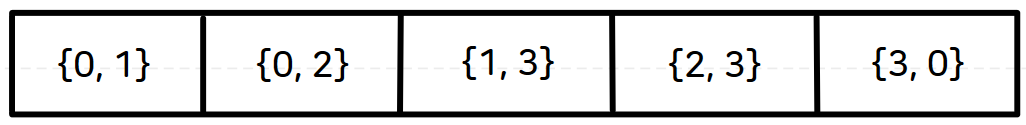
간선 리스트는 하나의 간선을 {시작 노드, 도착 노드} 형식으로 저장한다.
여기서 노드 A와 연결된 노드를 찾으려고 한다면, 간선 리스트 전체를 탐색하며 시작 노드가 A인 간선을 찾아야 할 것이다.
따라서, 간선 리스트 방식은 그래프 탐색에 있어서는 선호되는 방식은 아니다.
또한, 간선 리스트 방식은 노드를 기준으로 저장하는 것이 아닌 간선의 정보만 저장하는 방식이므로
간선이 없는 노드는 간선 리스트만으로 알 수 없다는 단점이 있다.
이러한 단점에도 불구하고 간선 리스트 방식이 쓰이는 이유는 간선을 기준으로 그래프를 해석할 때 매우 유용하기 때문이다.
이를 코드로 표현하면 다음과 같다.
만약, 위의 그래프가 양방향 그래프라면?
양방향 그래프 하나의 간선에 대해 방향 그래프 간선 2개로 생각하여 다음과 같이 표현하면 된다.

만약, 위의 그래프가 가중 그래프라면?
가중 그래프라면 간선에 대해서 가중치가 얼마인지를 함께 저장하면 된다.
가중 그래프가 아닌 경우의 간선 리스트에서는 {시작 노드, 도착 노드}만 저장했다면,
가중 그래프인 경우의 간선 리스트에서는 {시작 노드, 도착 노드, 간선의 가중치} 형태로 저장하면 된다.
정리
지금까지 그래프를 코드로 표현하는 방법 3가지에 대해서 알아보았다.
그렇다면, '방법이 3가지니까 아무 방법이나 쓰면 될까?'
그건 아니다. 각 상황마다 좋은 방법이 존재하기 때문에 이에 대해 간략하게 정리해보겠다.
인접 리스트
그래프를 코드로 표현할 때 이 방법을 기본(default)으로 생각하면 된다.
왜냐하면, 어떤 노드와 연결된 노드를 가장 쉽게 접근할 수 있으므로 그래프 탐색에 있어 편리하기 때문이다.
참고로, 인접 리스트 방식은 최단 경로 알고리즘의 '다익스트라' 알고리즘에서 쓰인다.
인접 행렬
인접 행렬같은 경우는 어떤 노드 A에서 어떤 노드 B로 가는 간선이 있는지를 빠르게 확인해야 할 때 사용하면 된다.
인접 행렬에서는 이를 adj_matrix[A][B]를 접근하여 $O(1)$만에 판단 가능하기 때문에 매우 효율적이다.
참고로, 인접 행렬 방식은 최단 경로 알고리즘의 '플로이드-워셜' 알고리즘에서 쓰인다.
간선 리스트
간선 리스트는 간선들을 기준으로 무언가를 처리해야할 때 쓰면 된다.
코딩테스트 문제 수준에서는 이러한 경우가 드물기 때문에 이러한 방법이 있다는 정도만 알아두자.
참고로, 간선 리스트 방식은 최단 경로 알고리즘의 '벨만-포드' 알고리즘에서 쓰인다.
요약하자면, 그래프를 코드로 표현할 때 인접 리스트를 주로 사용하며
인접 행렬과 간선 리스트는 '플로이드-워셜', '벨만-포드' 알고리즘을 쓰는 것이 아니면 거의 쓸 일이 없다!
하지만, 이 두 방법도 사용해야 하는 경우가 생길 수 있으니 여기에 나온 정도는 공부하길 바란다
궁금한 점이나 코멘트는 댓글로 남겨주세요!
- 알고리즘 공부법 : https://gliver.tistory.com/6
- 알고리즘 목차: https://gliver.tistory.com/7
'✏️ 알고리즘 > 그래프 알고리즘' 카테고리의 다른 글
| [18강] 최소 신장 트리 (MST) (2) | 2023.01.08 |
|---|---|
| [17강] 사이클이 없는 방향 그래프 (DAG) (2) | 2023.01.07 |
| [16강] 그래프(Graph) 최단 경로 알고리즘 (4) | 2023.01.07 |
| [15강] 그래프(Graph) 순회 (DFS & BFS) (2) | 2022.12.31 |
| [13강] 그래프(Graph)를 배우는 이유 (2) | 2022.12.25 |

![[14강] 그래프(Graph) 기본](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbuXXHW%2FbtrUSvdXiHG%2Fy0VkwnhyM490p2yzfjt1p1%2Fimg.png)