안녕하세요 Gliver 입니다.
이번 글에서는 그래프(Graph) 순회 (DFS & BFS)에 대해 알아보겠습니다.
목차
- 그래프 순회란?
- 깊이 우선 탐색 (DFS)
- 깊이 우선 탐색 (BFS)
- 정리
지난 글에서 그래프를 코드로 표현하는 법에 대해서 알아보았습니다.
이번 글에서는 어떻게 그래프를 순회(탐색)할 수 있는지 알아보겠습니다.
지난 글에서 말했듯이 그래프 탐색에 있어서는 인접 리스트 방식을 이용할 예정임
그래프 순회란?
그래프 순회(탐색)란 그래프 내의 모든 노드를 한 번씩 살펴보는 것을 의미한다.
선형 자료구조에서 탐색
선형 자료구조란 순서가 있는 자료구조를 의미한다.
즉, 배열 같은 경우는 원소들이 인덱스 순으로 구성되어 있으니 선형 자료구조라고 할 수 있다.
이러한 선형 자료구조에서의 탐색은 (인덱스) 순서대로 살펴보면 쉽게 수행할 수 있다.
하지만, 우리가 지금 살펴보는 그래프는 '노드간의 순서라는 개념이 존재하는가?'
조금 생각해보면 그렇지 않다는 것을 알 수 있을 것이다.
따라서, 비선형 자료구조인 그래프에서의 순회(탐색)를 할 때는 시작 노드를 설정해 주어야 한다.
이후에 시작노드를 기준으로 연결된 노드들을 살펴보며 그래프 순회(탐색)를 수행할 수 있는 것이다.
어떤 노드와 연결된 노드들은 그래프를 인접 리스트 방식으로 표현하면 쉽게 알 수 있다고 하였다
시작 노드를 기준으로 연결된 노드들을 살펴볼 때 살펴보는 방식에 따라 다음과 같이 두 가지로 분류할 수 있다.
깊이 우선 탐색 (DFS, Depth-Frist Search)
현재 탐색 중인 노드를 기준으로 연결된 노드를 즉시 방문하는 방식
너비 우선 탐색 (BFS, Breadth-First Search)
시작 노드를 기준으로 거리가 가까운 노드를 먼저 방문하는 방식
'시작 노드를 기준으로 거리가 가깝다'는 의미는 시작 노드에서 해당 노드까지 갈 때 거친 간선의 개수가 적다는 것을 의미
깊이 우선 탐색 (DFS)
깊이 우선 탐색(DFS)은 현재 탐색 중인 노드를 기준으로 연결된 노드를 즉시 방문하는 방식이라고 하였다.
다음과 같은 그래프에 대해서 시작 노드를 0으로 하여 깊이 우선 탐색(DFS)을 수행해 보자.
(참고로, 연결된 노드 중 무엇을 먼저 방문하냐에 따라서 방문 순서가 달라지므로 결과는 여러 종류 존재한다.)

깊이 우선 탐색(DFS)을 수행하면 다음과 같은 과정이 순서대로 일어난다.



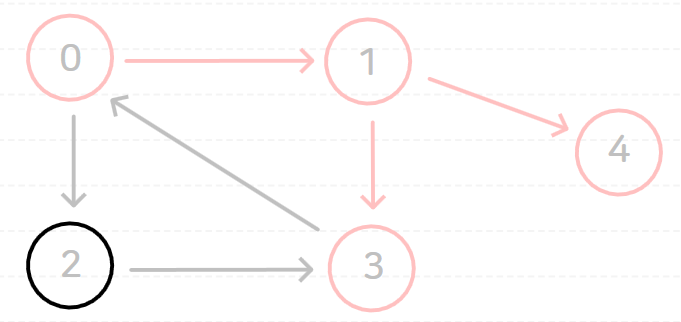

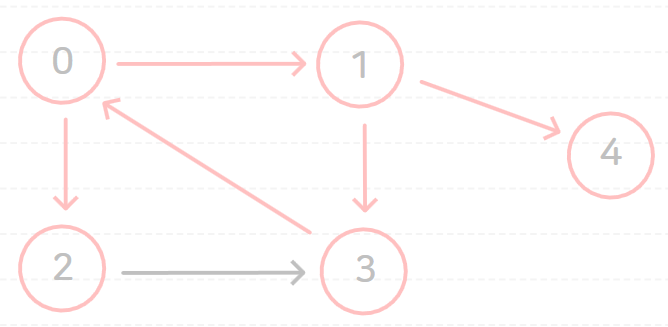


위와 같이 깊이 우선 탐색(DFS)을 할 경우에 0 → 1 → 4 → 3 → 2 순서로 방문하게 된다.
이를 코드로 구현할 때는 stack 자료구조를 쓰거나 재귀 함수를 통해서 구현하며 재귀 함수를 통해서 구현한 코드는 다음과 같다.
(adj_list는 인접 리스트를 의미하며, visited는 노드의 방문 여부를 체크하기 위한 배열이다.)
| #include <bits/stdc++.h> | |
| using namespace std; | |
| vector<vector<int>> adj_list(5); | |
| vector<bool> visited(5, false); | |
| // DFS function | |
| void dfs(int node) { | |
| if (visited[node]) return; | |
| visited[node] = true; | |
| cout << node << ' '; | |
| for (auto &adj_node : adj_list[node]) { | |
| dfs(adj_node); | |
| } | |
| } | |
| int main() | |
| { | |
| // Create Adjacency List | |
| adj_list[0].push_back(1); adj_list[0].push_back(2); | |
| adj_list[1].push_back(4); adj_list[1].push_back(3); | |
| adj_list[2].push_back(3); | |
| adj_list[3].push_back(0); | |
| // Execute Depth-First Search with start node '0' | |
| dfs(0); | |
| return 0; | |
| } |
| N = 5 # number of nodes | |
| # DFS function | |
| def dfs(node): | |
| global adj_list, visited | |
| # base case | |
| if visited[node]: | |
| return | |
| visited[node] = True | |
| print(node, end=' ') | |
| # recursive case | |
| for adj_node in adj_list[node]: | |
| dfs(adj_node) | |
| adj_list = [[] for _ in range(N)] | |
| visited = [False] * N | |
| # Create Adjacency List | |
| adj_list[0].append(1); adj_list[0].append(2) | |
| adj_list[1].append(4); adj_list[1].append(3) | |
| adj_list[2].append(3) | |
| adj_list[3].append(0) | |
| # Execute Depth-First Search with start node '0' | |
| dfs(0) |
dfs(node)는 node를 처음 방문하는 경우에만 방문하며 node와 연결된 모든 노드(adj_node)에 대해 dfs(adj_node)를 실행한다.
너비 우선 탐색 (BFS)
너비 우선 탐색(BFS)은 시작 노드를 기준으로 거리가 가까운 노드를 먼저 방문하는 방식이라고 하였다.
다음과 같은 그래프에 대해서 시작 노드를 0으로 하여 너비 우선 탐색(BFS)을 수행해 보자.
(시작 노드와 거리가 같은 노드들의 방문 순서는 바뀌어도 상관 없지만, 거리가 다르다면 가까운 노드를 먼저 방문해야 한다.)

너비 우선 탐색(BFS)을 수행하면 다음과 같은 과정이 순서대로 일어난다.




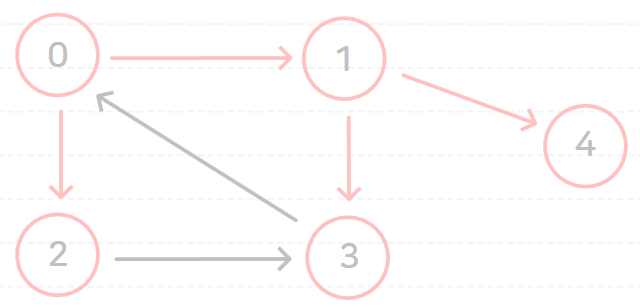

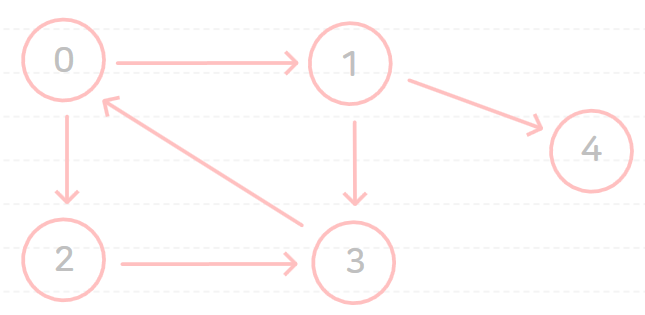

위와 같이 너비 우선 탐색(BFS)을 할 경우에 0 → 1 → 2 → 4 → 3 순서로 방문하게 된다.
이를 코드로 구현할 때는 queue 자료구조를 사용하여 구현하며 구현한 코드는 다음과 같다.
(adj_list는 인접 리스트를 의미하며, visited는 노드의 방문 여부를 체크하기 위한 배열이다.)
| #include <bits/stdc++.h> | |
| using namespace std; | |
| vector<vector<int>> adj_list(5); | |
| vector<bool> visited(5, false); | |
| int main() | |
| { | |
| // Create Adjacency List | |
| adj_list[0].push_back(1); adj_list[0].push_back(2); | |
| adj_list[1].push_back(4); adj_list[1].push_back(3); | |
| adj_list[2].push_back(3); | |
| adj_list[3].push_back(0); | |
| // Execute Breadth-First Search with start node '0' | |
| queue<int> q; | |
| q.push(0); | |
| visited[0] = true; | |
| while (!q.empty()) { | |
| int node = q.front(); q.pop(); | |
| cout << node << ' '; | |
| for (auto &adj_node : adj_list[node]) { | |
| if (visited[adj_node]) continue; | |
| q.push(adj_node); | |
| visited[adj_node] = true; | |
| } | |
| } | |
| return 0; | |
| } |
| from collections import deque | |
| N = 5 # number of nodes | |
| adj_list = [[] for _ in range(N)] | |
| visited = [False] * N | |
| # Create Adjacency List | |
| adj_list[0].append(1); adj_list[0].append(2) | |
| adj_list[1].append(4); adj_list[1].append(3) | |
| adj_list[2].append(3) | |
| adj_list[3].append(0) | |
| # Execute Breadth-First Search with start node '0' | |
| q = deque() | |
| q.append(0) | |
| visited[0] = True | |
| while q: | |
| node = q.popleft() | |
| print(node, end=' ') | |
| for adj_node in adj_list[node]: | |
| if visited[adj_node]: | |
| continue | |
| q.append(adj_node) | |
| visited[adj_node] = True | |
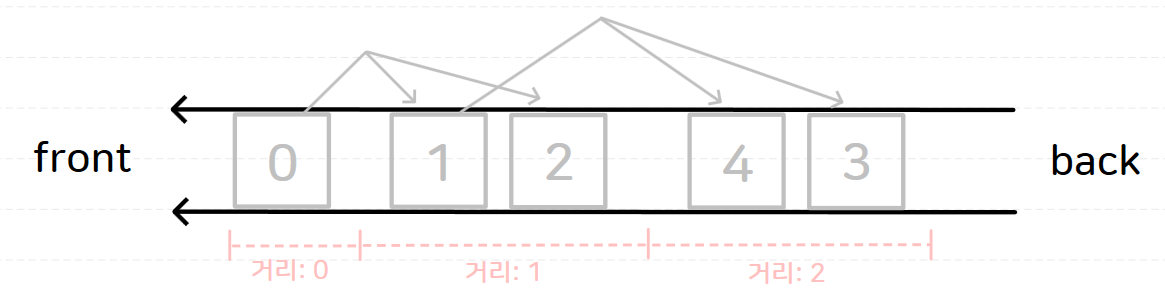
너비 우선 탐색(BFS)은 시작 노드로부터 거리가 가까운 노드 순으로 탐색한다고 하였다.
따라서, 선입 선출의 특징을 가지는 queue 자료구조를 이용하여 거리가 가까운 노드 순으로 탐색할 수 있다.
처음에는 queue에 시작 노드를 넣는다.
이후에 queue에 들어 있는 원소(노드)를 꺼내며 방문 처리를 하며 노드와 연결된 노드들을 queue에 넣어준다.
이렇게 하면 시작 노드로부터 가까운 노드를 먼저 방문하며 탐색할 수 있게 된다.
앞에서 살펴 본 예시에 대해 queue에 원소가 들어오고 나가는 순서를 그려보면 다음과 같다.
정리
지금까지 그래프를 순회(탐색)하는 법인 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)에 대해서 알아 보았다.
두 알고리즘 모두 노드와 간선을 한 번씩 처리하므로 시간 복잡도는 O(N+M) 이라고 할 수 있다. (N: 노드의 개수, M: 간선의 개수)
그렇다면 '그래프 순회(탐색)에 있어 두 알고리즘 중에서 아무거나 쓰면 될까?'
시간 복잡도가 동일하며 두 알고리즘 모두 그래프 순회(탐색)를 충실히 수행하는 알고리즘이므로 아무거나 쓰면 된다.
단, 시작 노드로부터 거리가 가까운 순으로 탐색해야 하는 경우라면 너비 우선 탐색(BFS)을 사용해야 한다!
이렇게만 보면 너비 우선 탐색(BFS)은 깊이 우선 탐색(DFS)을 완전히 대체할 수 있는 것처럼 보인다.
하지만, 깊이 우선 탐색(DFS)의 로직이 그래프 순회(탐색)의 가장 기초적인 로직이며 구현 또한 직관적이라는 장점이 있다.
정리하면, DFS와 BFS 중에서 본인이 쉽다고 생각하는 알고리즘 1개만 공부하여 주로 사용하면 된다.
단, 시작 노드로부터 거리가 가까운 순으로 탐색해야 하는 경우는 꼭 BFS를 이용해야 한다는 점을 잊지 말자
나 같은 경우에도, 기본적인 탐색만 해도 되는 경우면 DFS를 사용하며, 거리가 가까운 순으로 탐색해야 하는 경우일 때는 BFS를 사용한다.
[관련 문제]
궁금한 점이나 코멘트는 댓글로 남겨주세요!
- 알고리즘 공부법 : https://gliver.tistory.com/6
- 알고리즘 목차: https://gliver.tistory.com/7
'✏️ 알고리즘 > 그래프 알고리즘' 카테고리의 다른 글
| [18강] 최소 신장 트리 (MST) (2) | 2023.01.08 |
|---|---|
| [17강] 사이클이 없는 방향 그래프 (DAG) (2) | 2023.01.07 |
| [16강] 그래프(Graph) 최단 경로 알고리즘 (4) | 2023.01.07 |
| [14강] 그래프(Graph) 기본 (0) | 2022.12.30 |
| [13강] 그래프(Graph)를 배우는 이유 (2) | 2022.12.25 |

![[15강] 그래프(Graph) 순회 (DFS & BFS)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FEwdHB%2FbtrU005Mw7p%2FNjkq4QGfswtzt33aEMgw6k%2Fimg.png)