안녕하세요 Gliver 입니다.
이번 글에서는 그래프(Graph) 최단 경로 알고리즘에 대해 알아보겠습니다.
목차
- 그래프에서 최단 경로란?
- 다익스트라 알고리즘
- 벨만-포드 알고리즘
- 플로이드-워셜 알고리즘
- 정리
지난 글에서 그래프를 순회(탐색)하는 법에 대해서 알아보았습니다.
이번 글에서는 그래프의 최단 경로를 구하는 알고리즘에 대해 알아보겠습니다.
그래프에서 최단 경로란?
그래프에서 최단 경로란 어떤 노드 A에서 어떤 노드 B까지의 최단 경로를 의미한다.
즉, A에서 B로 가는 다양한 경로가 있다면 그중에서 거리가 가장 짧은 거리를 최단 거리라 하며 그때의 경로를 최단 경로라고 한다.
거리가 짧다는 것의 기준은 무엇일까?
가중 그래프가 아닌 경우에는 경로 상에 있는 간선의 수가 적을수록 거리가 짧다는 것을 의미하며
가중 그래프인 경우에는 경로 상에 있는 간선의 가중치 합이 작을수록 거리가 짧다는 것을 의미한다.
최단 경로는 항상 정의될 수 있는가?

위 그림에서 노드 1에서 노드 3까지의 최단 거리, 최단 경로를 찾아보자.
단순하게 보면 1→2→3이 최단 경로이며 따라서 최단 거리는 3인 거 같다.
하지만, 이는 틀렸다. 왜냐하면, 1→2→3→1→2→3인 경로의 거리는 2이기 때문이다.
1→2→3 사이클을 거치면 거칠수록 경로의 거리가 줄어드는 구조이므로 최단 거리가 계속 작아질 수 있다.
여기서 살펴봤듯이, 사이클이 존재하며 그 사이클이 음수 사이클이라면 최단 거리가 정의될 수 없다.
여기서, 음수 사이클이란 사이클 내에 있는 간선의 가중치 합이 음수인 사이클을 의미한다.
위 예시의 경우에 사이클 내에 있는 간선의 가중치 합이 -1(=5-4-2)이므로 음수 사이클에 해당한다
음수 사이클이 없는 경우에 최단 경로/거리가 정의되며, 이때 최단 경로/거리를 구하는 알고리즘은 다음과 같이 3가지 존재한다.
최단 경로 알고리즘이 3가지나 존재하는 이유는 각각의 알고리즘을 사용할 수 있는 환경이나 결과물이 다르기 때문이다
- 다익스트라 (Dijkstra) 알고리즘
- 벨만-포드 (Bellman-Ford) 알고리즘
- 플로이드-워셜 (Floyd-Warshall) 알고리즘
본 글에서는 3가지 알고리즘을 이용하여 최단 거리를 구하는 것을 중점적으로 설명하겠습니다.
최단 경로를 구하는 것은 최단 거리를 구하는 알고리즘에서 조금의 처리만 해주면 되며 이와 관련한 내용은 추후에 올리겠습니다.
다익스트라 알고리즘
다익스트라 알고리즘은 한 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘으로 그리디한 성질을 갖는다.
다익스트라 알고리즘은 음수 간선이 존재하지 않을 때만 사용할 수 있다.
다익스트라 알고리즘은 한 노드를 정하고 그 노드를 시작으로 하여 거리가 짧은 경로들을 우선적으로 탐색하는 것이다.
어떠한 경로 'a→b→c'와 'a→b→c→α→c'가 있다고 해보자.
음수 간선이 없는 환경에서 'a→b→c'의 경로는 'a→b→c→α→c'의 경로보다 항상 거리가 짧다는 것을 이해할 수 있을 것이다.
즉, 음수 간선이 없는 환경에서는 한 노드를 기준으로 가장 짧은 거리의 경로부터 탐색하면 그 경로가 최단 경로가 되는 것이다!
다음과 같은 그래프가 있을 때 노드 0을 기준으로 다익스트라 알고리즘을 수행해 보자.

노드 0을 기준으로 다익스트라 알고리즘을 수행하면 다음과 같은 과정이 순서대로 일어난다.

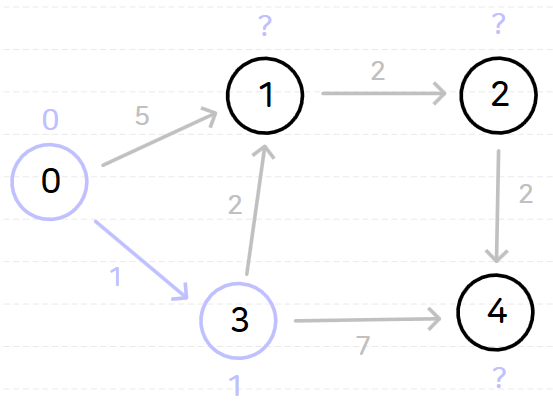
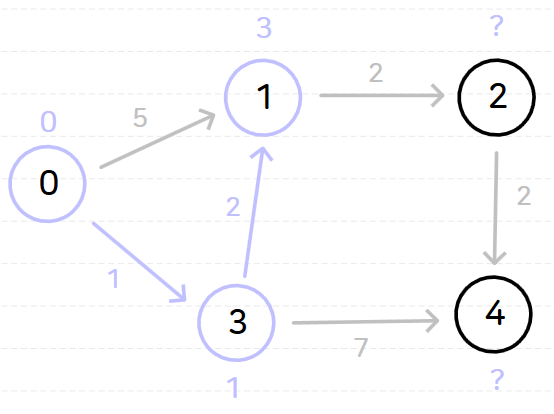
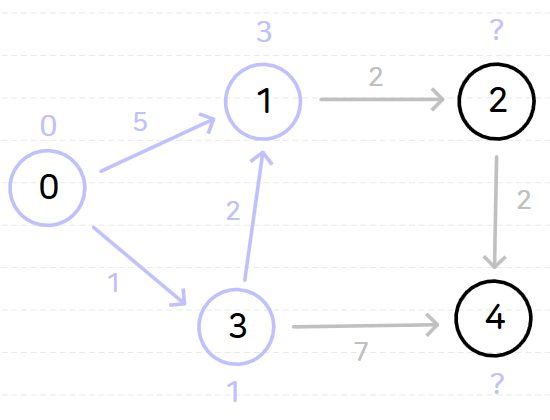
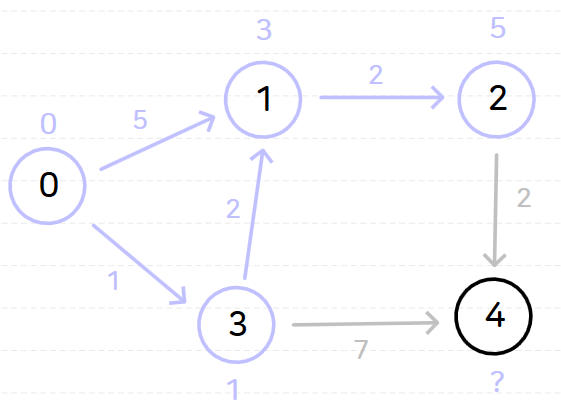
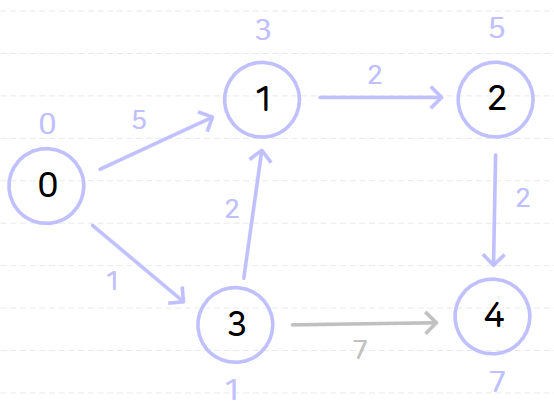
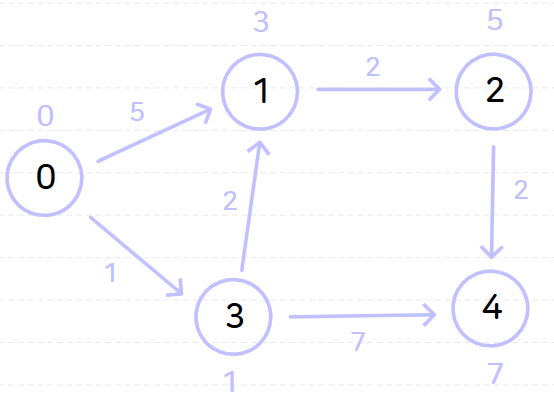
위와 같이 다익스트라 알고리즘을 시행하고 나면 노드 0으로부터 다른 모든 노드까지의 최단 거리는 다음과 같이 나온다.
- 0→0: 0
- 0→1: 3
- 0→2: 5
- 0→3: 1
- 0→4: 7
다익스트라 알고리즘의 핵심은 기준 노드로부터 가장 짧은 거리의 경로부터 탐색한다는 것이다.
이렇게 해서 도착한 노드들은 무조건 처음 방문했을 때가 그 노드까지의 최단 경로가 되는 것이다.
가장 짧은 거리의 경로 순으로 탐색하려면 탐색을 하려는 경로의 후보 중에서 거리가 가장 짧은 경로를 뽑아야 한다.
이를 구현하기에 있어 가장 적합한 자료구조는 heap(priority queue)이고, 이를 활용하여 구현한 코드는 다음과 같다.
(dist는 기준 노드로부터의 최단 거리를 저장하는 배열이며, pq는 minimum heap 자료구조이다.)
| #include <bits/stdc++.h> | |
| using namespace std; | |
| const int INF = int(1e9); | |
| int main() | |
| { | |
| int N = 5; | |
| vector<vector<array<int,2>>> adj_list(N); | |
| vector<int> dist(N, INF); | |
| // Create Adjacency List | |
| adj_list[0].push_back({1, 5}); adj_list[0].push_back({3, 1}); | |
| adj_list[1].push_back({2, 2}); | |
| adj_list[2].push_back({4, 2}); | |
| adj_list[3].push_back({1, 2}); adj_list[3].push_back({4, 7}); | |
| // Execute Dijkstra Alogrithm with standard node '0' | |
| priority_queue<array<int,2>, vector<array<int,2>>, greater<array<int,2>>> pq; | |
| pq.push({0, 0}); | |
| dist[0] = 0; | |
| while (!pq.empty()) { | |
| int cur_dist = pq.top()[0]; | |
| int cur_node = pq.top()[1]; | |
| pq.pop(); | |
| if (cur_dist > dist[cur_node]) continue; | |
| for (auto &[adj_node, adj_dist] : adj_list[cur_node]) { | |
| temp_dist = cur_dist + adj_dist; | |
| if (temp_dist < dist[adj_node]) { | |
| pq.push({temp_dist, adj_node}); | |
| dist[adj_node] = temp_dist; | |
| } | |
| } | |
| } | |
| // Print result | |
| for (int i=0; i<N; i++) { | |
| cout << dist[i] << ' '; | |
| } | |
| return 0; | |
| } |
| from queue import PriorityQueue | |
| INF = int(1e12) | |
| N = 5 | |
| adj_list = [[] for _ in range(N)] | |
| dist = [INF] * N | |
| # Create Adjacency List | |
| adj_list[0].append([1, 5]); adj_list[0].append([3, 1]); | |
| adj_list[1].append([2, 2]) | |
| adj_list[2].append([4, 2]) | |
| adj_list[3].append([1, 2]); adj_list[3].append([4, 7]); | |
| # Execute Dijkstra Algorithm with standard(start) node '0' | |
| pq = PriorityQueue() | |
| pq.put([0, 0]) | |
| dist[0] = 0 | |
| while not pq.empty(): # pq.queue | |
| cur_dist, cur_node = pq.get() | |
| if cur_dist > dist[cur_node]: | |
| continue | |
| for adj_node, adj_dist in adj_list[cur_node]: | |
| temp_dist = cur_dist + adj_dist | |
| if temp_dist < dist[adj_node]: | |
| pq.put([temp_dist, adj_node]) | |
| dist[adj_node] = temp_dist | |
| # Print result | |
| print(dist) |
dist[node]가 INF이면 기준 노드로부터 node까지의 최단 거리가 확정되지 않은 상태임을 의미하고
dist[node]가 INF이 아니라면 기준 노드로부터 node까지의 최단 거리가 dist[node] 값으로 확정된 상태임을 의미한다.
다익스트라 알고리즘은 경로의 후보를 heap에 저장해야 하므로 시간 복잡도는 O(M⋅logN)이다. (N: 노드의 개수, M: 간선의 개수)
벨만-포드 알고리즘
벨만-포드 알고리즘은 한 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘으로 브루트 포스적인 성질을 갖는다.
벨만-포드 알고리즘은 음수 사이클이 존재하지 않을 때 사용할 수 있다.
벨만-포드 알고리즘은 한 노드를 정하고 간선 리스트를 이용하여 최단 경로의 후보를 모두 탐색하는 알고리즘이다.
노드의 개수를 N개라고 할 때, 벨만-포드 알고리즘은 N-1번의 step을 거치며 수행한다.
만약 k번 step을 시행했다면, 기준 노드로부터 k개의 노드를 거쳐 나올 수 있는 최단 거리를 찾은 상태이다.
다음과 같은 그래프가 있을 때 노드 0을 기준으로 벨만-포드 알고리즘을 수행해 보자.
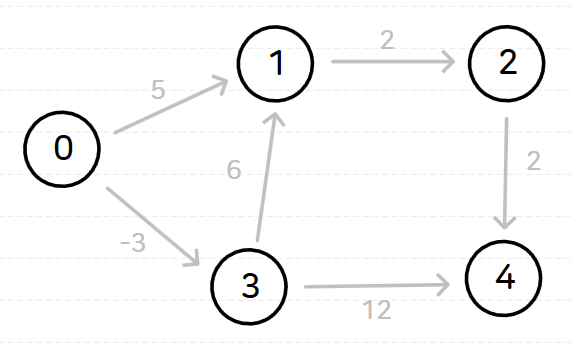
노드 0을 기준으로 벨만-포드 알고리즘을 수행하면 다음과 같은 과정이 순서대로 일어난다.
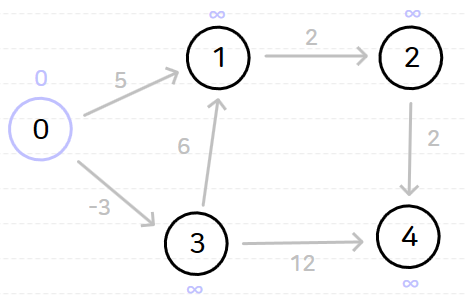
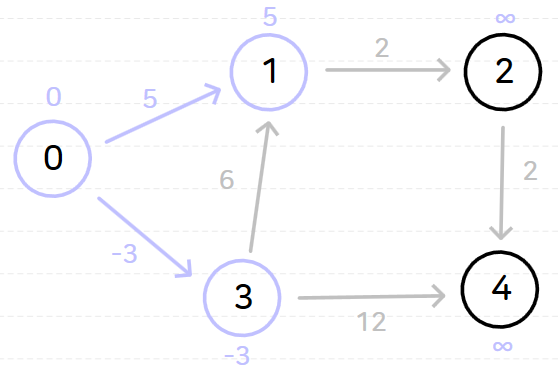
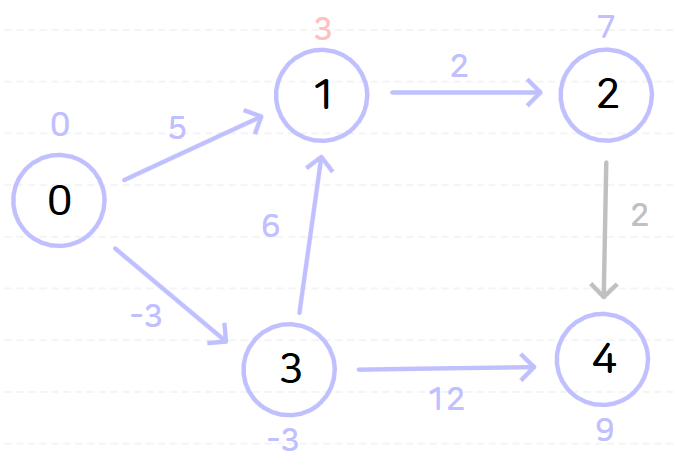
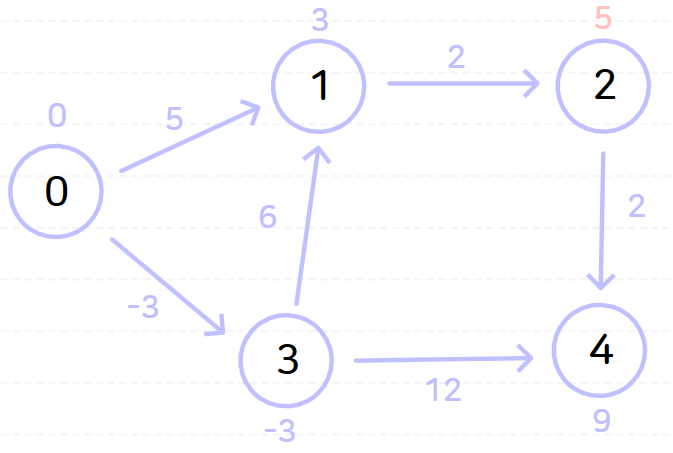
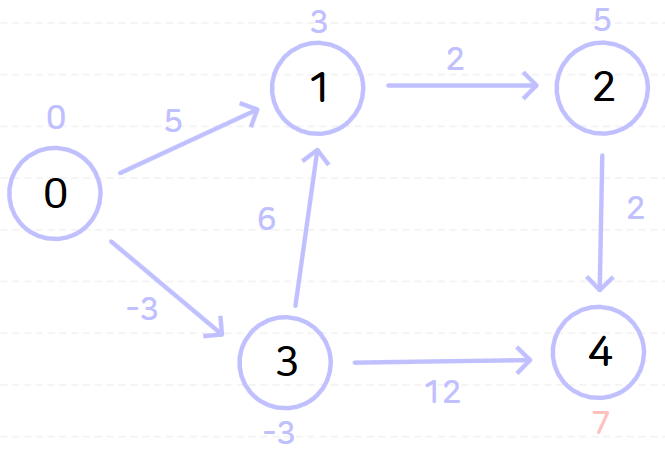
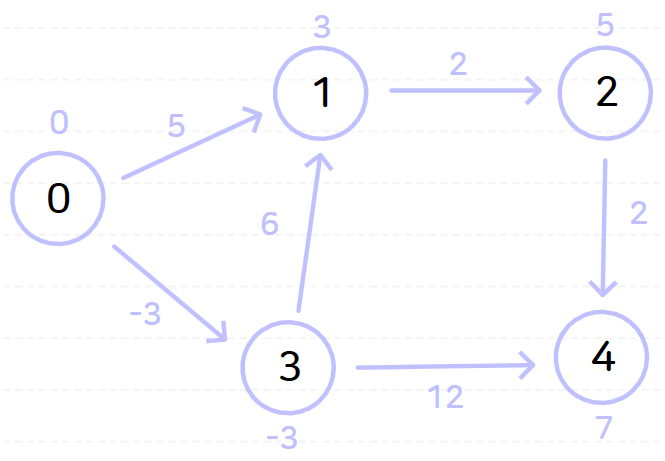
위와 같이 벨만-포드 알고리즘을 시행하고 나면 노드 0으로부터 다른 모든 노드까지의 최단 거리는 다음과 같이 나온다.
- 0→0: 0
- 0→1: 3
- 0→2: 5
- 0→3: -3
- 0→4: 7
벨만-포드 알고리즘은 한 번의 step에서 모든 간선을 살펴보며 최단 경로/거리를 계속 갱신해 나간다.
step을 k번 시행했다면, 기준 노드로부터 k개의 노드를 거쳐서 나올 수 있는 최단 경로/거리를 모두 찾은 상태이다.
어떠한 최단 경로가 아무리 길어봤자 노드를 N-1개 거치므로, step을 N-1번 거치면 모든 최단 경로/거리를 구할 수 있다.
즉, step을 N-1번 시행한 후에 한 번 더 step을 시행하더라도 갱신이 일어나지 않는다.
만약, N번째 step에서 갱신이 일어난다면 그것은 음수 사이클이 존재하여 갱신이 일어나는 것이다.
이를 구현하는 법은 간선 리스트로 그래프를 표현한 후에 한 번의 step에서 간선 리스트를 탐색하며 최단 거리를 갱신하면 된다.
step을 N-1번 시행하면 기준 노드로부터 다른 모든 노드까지의 최단 경로/거리를 구할 수 있다.
(dist는 기준 노드로부터의 최단 거리를 저장하는 배열이며, INF는 ∞를 표현한 큰 숫자이다.)
| #include <bits/stdc++.h> | |
| using namespace std; | |
| const int INF = 1e9; | |
| int main() | |
| { | |
| int N = 5; | |
| vector<array<int,3>> edge_list; | |
| vector<int> dist(N, INF); | |
| // Create Edge List | |
| edge_list.push_back({0, 1, 5}); | |
| edge_list.push_back({0, 3, -3}); | |
| edge_list.push_back({1, 2, 2}); | |
| edge_list.push_back({2, 4, 2}); | |
| edge_list.push_back({3, 1, 6}); | |
| edge_list.push_back({3, 4, 12}); | |
| // Execute Bellman-Ford Alogrithm with standard node '0' | |
| dist[0] = 0; | |
| for (int i=1; i<=N-1; i++) { // step i | |
| for (auto [start, end, weight] : edge_list) { | |
| if (dist[start] == INF) continue; | |
| dist[end] = min(dist[end], dist[start]+weight); | |
| } | |
| } | |
| // Print result | |
| for (int i=0; i<N; i++) { | |
| cout << dist[i] << ' '; | |
| } | |
| return 0; | |
| } |
| INF = int(1e9) | |
| N = 5 | |
| edge_list = [] | |
| dist = [INF] * N | |
| # Create Edge List | |
| edge_list.append([0, 1, 5]) | |
| edge_list.append([0, 3, -3]) | |
| edge_list.append([1, 2, 2]) | |
| edge_list.append([2, 4, 2]) | |
| edge_list.append([3, 1, 6]) | |
| edge_list.append([3, 4, 12]) | |
| # Execute Bellman-Ford Alogrithm with standard node '0' | |
| dist[0] = 0 | |
| for i in range(1, N): # step i | |
| for start, end, weight in edge_list: | |
| if start == INF: | |
| continue | |
| dist[end] = min(dist[end], dist[start]+weight) | |
| # Print result | |
| print(dist) |
벨만-포드 알고리즘은 step을 N-1번 시행하며 각 step에서 간선 리스트를 한 번 탐색하므로 시간 복잡도는 O(N⋅M)이다.
(N: 노드의 개수, M: 간선의 개수)
플로이드-워셜 알고리즘
플로이드-워셜 알고리즘은 모든 노드에서 모든 노드까지의 최단 경로를 구하는 알고리즘으로 브루트 포스적인 성질을 갖는다.
플로이드-워셜 알고리즘은 음수 사이클이 존재하지 않을 때 사용할 수 있다.
플로이드-워셜 알고리즘은 인접 행렬을 사용하고 노드를 기준으로 동작하는 알고리즘이며
모든 노드를 중간 지점으로 하여(N가지 경우) 모든 노드 쌍을 살펴보는(N²가지 경우) 알고리즘이다.
따라서, N³ 만큼의 연산이 걸리며 모든 경우를 살펴보는 알고리즘이라고 생각하면 된다.
다음과 같은 그래프가 있을 때 플로이드-워셜 알고리즘을 수행해 보자.

플로이드-워셜 알고리즘을 수행하고 나면 결과는 다음과 같다.
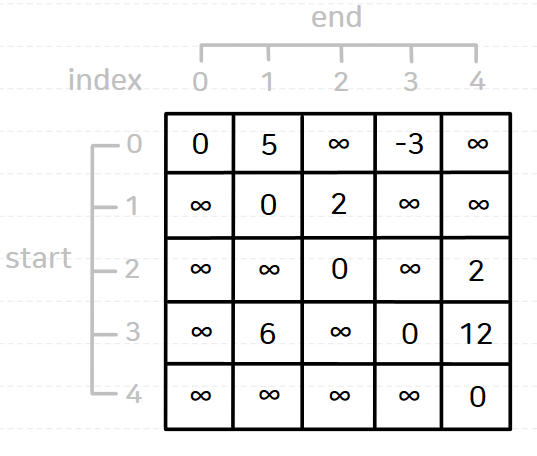
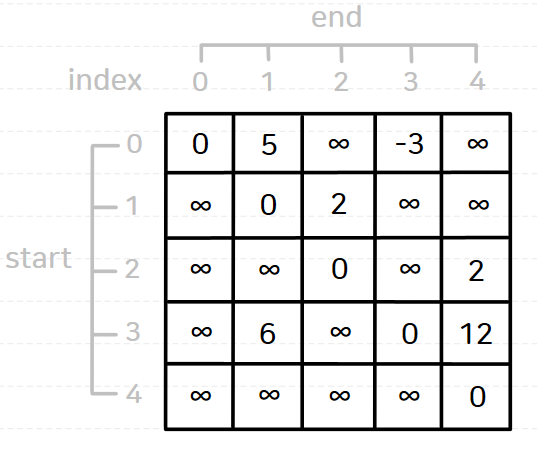

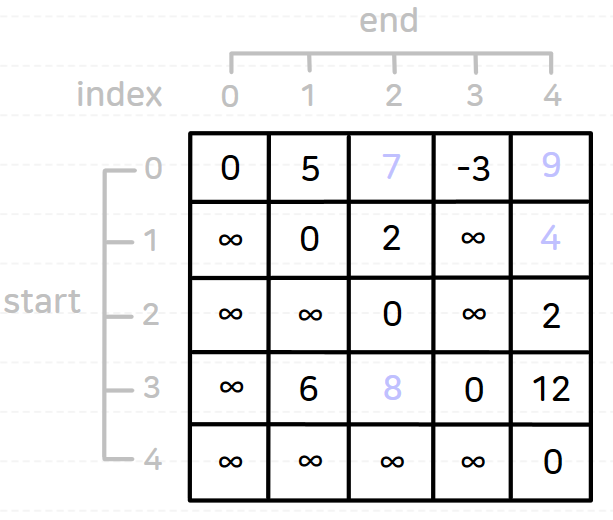
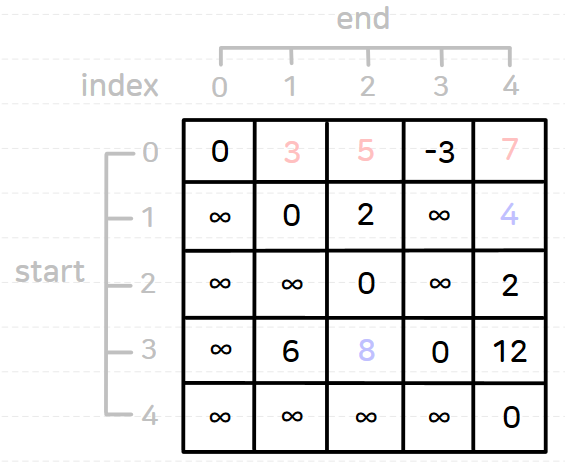
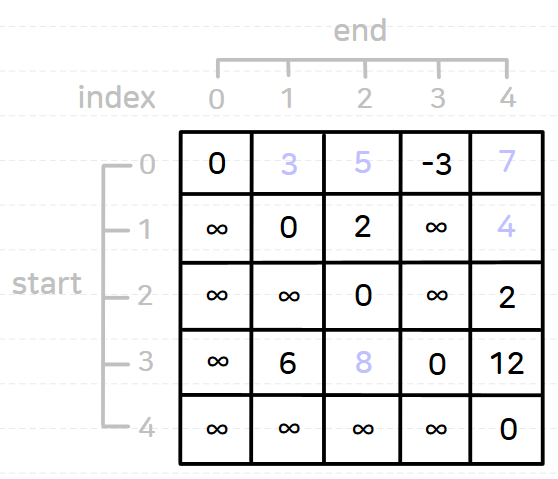
플로이드-워셜 알고리즘의 핵심 로직은 다음과 같다.
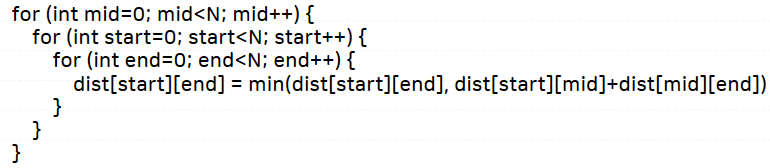
즉, 모든 노드를 중간 지점으로 하여(N가지 경우) 모든 노드 쌍을 살펴보며(N²가지 경우) 최단 경로/거리를 갱신하는 것이다.
이렇게 했을 때 모든 노드 간의 최단 경로/거리를 구할 수 있는 이유는 다음을 참고하기 바란다.
플로이드-워셜 알고리즘의 갱신 과정에서 dist[start][mid]와 dist[mid][end]가 ∞가 아니라면 start→mid→end 경로는 유효하다.
그리고, 알고리즘 진행 과정에서 유효한 start→mid→end 경로가 최단 경로/거리 갱신을 일으킨다.
어떤 노드 A에서 어떤 노드 B까지의 최단 경로에서 거치는 노드의 종류는 최대 N-2개이다.
따라서, 모든(N개의) 노드를 중간 지점으로 하여 알고리즘을 수행하면 어떤 노드 A에서 어떤 노드 B까지의 최단 경로/거리는 항상 발견된다!
예를 들어, 노드 0에서 노드 4까지의 최단 경로가 아래의 핑크색 경로라고 해보자.
이때, 중간 노드를 1, 2, 3으로 하여 알고리즘을 수행하면 해당 경로는 발견된다는 것이다.
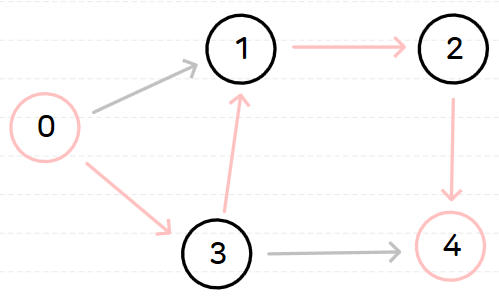
이를 구현하는 법은 인접 행렬로 그래프를 표현하고 이를 토대로 초기 dist배열을 만들고 위의 핵심 로직을 수행하면 된다.
(dist[A][B]는 노드 A에서 노드 B로 가는 최단 거리를 담고 있다.)
| #include <bits/stdc++.h> | |
| using namespace std; | |
| const int INF = 1e9; | |
| int main() | |
| { | |
| int N = 5; | |
| vector<vector<int>> adj_matrix(N, vector<int>(N, 0)); | |
| // Create Adjacency Matrix | |
| adj_matrix[0][1] = 5; adj_matrix[0][3] = -3; | |
| adj_matrix[1][2] = 2; | |
| adj_matrix[2][4] = 2; | |
| adj_matrix[3][1] = 6; | |
| adj_matrix[3][4] = 12; | |
| // Create dist array | |
| auto dist = adj_matrix; | |
| for (int i=0; i<N; i++) { | |
| for (int j=0; j<N; j++) { | |
| if (dist[i][j] == 0 && i != j) dist[i][j] = INF; | |
| } | |
| } | |
| // Execute Floyd-Warshall Algorithm | |
| for (int mid=0; mid<N; mid++) { | |
| for (int start=0; start<N; start++) { | |
| for (int end=0; end<N; end++) { | |
| if (dist[start][mid] == INF || dist[mid][end] == INF) continue; | |
| dist[start][end] = min(dist[start][end], dist[start][mid]+dist[mid][end]); | |
| } | |
| } | |
| } | |
| // Print result | |
| for (int i=0; i<N; i++) { | |
| for (int j=0; j<N; j++) { | |
| if (dist[i][j] == INF) cout << "∞" << ' '; | |
| else cout << dist[i][j] << ' '; | |
| } | |
| cout << '\n'; | |
| } | |
| return 0; | |
| } |
| import copy | |
| INF = int(1e9); | |
| N = 5 | |
| adj_matrix = [[0]*N for _ in range(N)] | |
| # Create Adjacency Matrix | |
| adj_matrix[0][1] = 5; adj_matrix[0][3] = -3 | |
| adj_matrix[1][2] = 2 | |
| adj_matrix[2][4] = 2 | |
| adj_matrix[3][1] = 6 | |
| adj_matrix[3][4] = 12 | |
| # Create dist array | |
| dist = copy.deepcopy(adj_matrix) | |
| for i in range(N): | |
| for j in range(N): | |
| if dist[i][j] == 0 and i != j: | |
| dist[i][j] = INF; | |
| # Execute Floyd-Warshall Algorithm | |
| for mid in range(N): | |
| for start in range(N): | |
| for end in range(N): | |
| if dist[start][mid] == INF or dist[mid][end] == INF: | |
| continue | |
| dist[start][end] = min(dist[start][end], dist[start][mid]+dist[mid][end]) | |
| # Print result | |
| for d in dist: | |
| for num in d: | |
| print(num if num != INF else '∞', end=' ') | |
| print() |
플로이드-워셜 알고리즘은 모든 노드를 중간 노드로 하여 모든 쌍을 살펴보므로 시간 복잡도는 O(N3)이다. (N: 노드의 개수)
정리
이제, 앞에서 배웠던 최단 경로 알고리즘 3가지에 대해 각각을 언제 써야 하는지 알아보도록 하자.
알고리즘 수행 결과물
- 다익스트라 알고리즘: 한 노드에서 다른 모든 노드까지의 최단 경로/거리
- 벨만-포드 알고리즘: 한 노드에서 다른 모든 노드까지의 최단 경로/거리
- 플로이드-워셜 알고리즘: 모든 노드에서 모든 노드까지의 최단 경로/거리
사용할 수 있는 환경
- 다익스트라 알고리즘: 음수 간선이 존재하지 않을 때
- 벨만-포드 알고리즘: 음수 사이클이 존재하지 않을 때
- 플로이드-워셜 알고리즘: 음수 사이클이 존재하지 않을 때
시간 복잡도
N은 노드의 개수를 의미하며, M은 간선의 개수를 의미한다.
(알고리즘의 효율성은 다익스트라, 벨만-포드, 플로이드-워셜 순이다.)
- 다익스트라 알고리즘: O(M⋅logN)
- 벨만-포드 알고리즘: O(N⋅M)
- 플로이드-워셜 알고리즘: O(N3)
문제를 보고 문제에서 요구하는 게 무엇인지를 살펴보면 어떤 알고리즘을 사용해야 할지 금방 알 수 있을 것이다.
이해를 돕기 위해서 몇 가지 예상되는 경우를 살펴보겠다.
Case1. 한 노드에서 다른 (모든) 노드까지의 최단 경로/거리 (음수 간선 존재 X)
한 노드에서 다른 (모든) 노드까지의 최단 경로/거리를 구해야 하므로 다익스트라 알고리즘 또는 벨만-포드 알고리즘을 쓸 수 있다.
조건에서 음수 간선이 존재하지 않으므로, 더 효율적인 다익스트라 알고리즘을 사용하면 된다.
Case2. 한 노드에서 다른 (모든) 노드까지의 최단 경로/거리 (음수 간선 존재 O)
한 노드에서 다른 (모든) 노드까지의 최단 경로/거리를 구해야 하므로 다익스트라 알고리즘 또는 벨만-포드 알고리즘을 써야 한다.
조건에서 음수 간선이 존재하므로 벨만-포드 알고리즘을 사용해야 한다.
Case3. 모든 노드에서 모든 노드까지의 최단 경로/거리
모든 노드에서 모든 노드까지의 최단 경로/거리를 구해야 하므로 플로이드-워셜 알고리즘을 쓰면 된다.
다익스트라 알고리즘이나 벨만-포드 알고리즘을 N번 수행하여 구할 수도 있으나 보통은 플로이드-워셜 알고리즘이 더 효율적이다
[관련 문제]
궁금한 점이나 코멘트는 댓글로 남겨주세요!
- 알고리즘 공부법 : https://gliver.tistory.com/6
- 알고리즘 목차: https://gliver.tistory.com/7
'✏️ 알고리즘 > 그래프 알고리즘' 카테고리의 다른 글
| [18강] 최소 신장 트리 (MST) (2) | 2023.01.08 |
|---|---|
| [17강] 사이클이 없는 방향 그래프 (DAG) (2) | 2023.01.07 |
| [15강] 그래프(Graph) 순회 (DFS & BFS) (2) | 2022.12.31 |
| [14강] 그래프(Graph) 기본 (0) | 2022.12.30 |
| [13강] 그래프(Graph)를 배우는 이유 (2) | 2022.12.25 |

![[16강] 그래프(Graph) 최단 경로 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FmgAVj%2FbtrVBdW3X32%2F2Ndy6oXGdikiorUkUn8tNK%2Fimg.png)